Nail Projectile Motion: 4 Mistakes You Don’t Want to Make!

Projectile Motion

Projectile motion might seem simple at first; it's just something that flies through the air, right? But once you start solving problems, it can get a bit tricky, and there are some common mistakes that trip up a lot of students. If you’ve ever found yourself stuck wondering why your numbers aren’t adding up, don’t worry; you’re not alone.

Let’s break down projectile motion step by step, and point out the four biggest mistakes people make when solving these problems. By the end of this, you’ll not only understand projectile motion better, but you’ll also know exactly what to look out for!

Mistake 1: Forgetting the Horizontal Component Has No Acceleration

Here’s something a lot of people get wrong: The horizontal motion has no acceleration. This means that the horizontal velocity is constant throughout the motion. Why? Because there’s no force acting in the horizontal direction (we’re ignoring air resistance here).

So, what does this mean for your calculations? The only equation you’ll ever need for horizontal motion is:

v = Δd/t

That’s it! Simple, right? Horizontal velocity doesn’t change, so no need to overcomplicate things. Just remember that if you’re solving for the horizontal distance or time, you’re using this formula.

Mistake 2: Thinking All Velocity is Zero at the Top

Another super common mistake: thinking that the velocity is zero at the top of the projectile’s path. Let me be clear: only the vertical velocity is zero at the highest point.

Why is that? Think about it: at the top, the object has reached its maximum height, so it’s momentarily stopped moving up or down. But, it’s still moving horizontally! Remember, the horizontal velocity is constant, so it never goes to zero unless some external force (like a wall or the ground) stops it.

In short:

• At the very top, vertical velocity = 0.

• But horizontal velocity is still going strong (and equal to the initial horizontal velocity)!

Mistake 3: Ignoring Final Velocity

Here’s another one I see all the time: thinking there’s no final velocity just because the object hits the ground. Wrong! The object definitely has a final velocity; it doesn’t just stop in midair. When it hits the ground, it has a certain velocity that combines both the horizontal and vertical components, and then it may slow down due to friction or other forces.

So, even though the object eventually comes to a stop, it definitely hits the ground with a final velocity. You can calculate this by combining the horizontal velocity (which hasn’t changed) and the final vertical velocity (using the usual kinematic equations).

Mistake 4: Forgetting Projectile Motion is Symmetrical

Here’s the beauty of projectile motion: it’s symmetrical. What does that mean? If you imagine drawing a vertical line down the centre of the motion, any two points on opposite sides of that line will have the same velocity, but with opposite signs.

For example, let’s say an object is launched upward at 20 m/s. When it comes back down to the same height, its velocity will also be 20 m/s, but in the opposite direction (downward). This symmetry makes solving problems easier because once you know how fast something is moving on the way up, you know exactly how fast it’s moving on the way down; just reverse the sign.

A Quick Example

Let’s say you launch a ball with an initial velocity of 15 m/s at a 45° angle. Let’s solve this using what we’ve just learned:

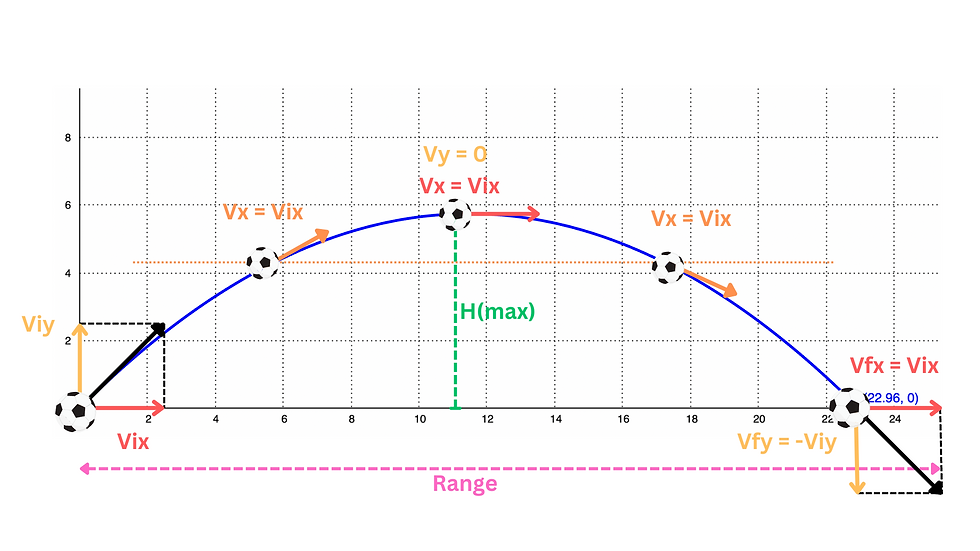
1. Break it into components:

   X: Horizontal velocity: 15 cos(45°)=10.6 m/s

   Y: Vertical velocity: 15 sin(45°)=10.6 m/s

   
   

2. Time to the top:

   Vertical velocity at the top = 0 = vf

   Time up:  vf=vi + at

     0 = 10.6 + -9.81t

                  t = 10.6/9.81=1.08 s

   
   

3. Total time in the air:

   Since the motion is symmetrical, the total time = time up × 2 = 1.08 × 2 = 2.16 seconds.

   
   

4. Range (horizontal distance):

   Range = horizontal velocity × total time = 10.6×2.16≈22.96 meters

   
   

5. Final velocity:

   At the moment the ball hits the ground, the horizontal velocity is still 10.6 m/s, and the vertical velocity is -10.6 m/s (same magnitude as the initial, but downward). The total final velocity is a combination of these two.

   
   

The Bottom Line: Watch Out for These Mistakes!

Projectile motion becomes so much easier once you know the common traps to avoid:

1. Horizontal velocity doesn’t change; there’s no acceleration, so, v = dt is all you need.

2. At the top of the path, only the vertical velocity is zero; the horizontal velocity keeps going.

3. Final velocity exists; just because something hits the ground doesn’t mean it stops instantly.

4. Projectile motion is symmetrical; the velocity on the way up equals the velocity on the way down (with opposite signs).

By keeping these in mind, you’ll be able to solve projectile motion problems more confidently and avoid the mistakes that trip up so many students. Now go ace those physics problems!